OpenSSL better than Intel IPP
Recently I was in a need to generate a lot of RSA keys. As a true scientist in the making, I decided to do my research, and investigate the prior work. The simple solution was to use OpenSSL and use the builtin RSA_generate_key / RSA_generate_key_ex functions. However, I needed the generation of RSA keys to be as fast as possible.
As my use case for generating RSA keys was not imposing any dependencies between the generated keys, I classified my problem as embarrassingly parallel and I even considered GPUs as a possible possible alternative. The Fair Comparison between CPU and GPU, at the time of the writing, suggests that a hexa-core CPU could match the performance of GTX580. Since on my disposal I have an Intel(R) Xeon(R) CPU E3-1285L v3 @ 3.10GHz and an NVIDIA GT640, I decided to go with a CPU solution. The same article (also at the time of the writing) suggests that Intel IPP implementation would beat everything else, by a huge margin. Therefore I stared the first implementation using Intel IPP Cryptography Libraries.
Intel IPP is quite modular, and the implementation for generating RSA private and public key pair is not as simple as the one of OpenSSL, requiring a deep dive into the documentation provided by Intel. After finding my way through initializing a Pseudo Random Generator, Prime Number Generator, and calculating the bit sizes of the P and Q factors, I finally got to the initial implementation.
While in OpenSSL, RSA keys can be generated using:
RSA_generate_key(bitsRSA, publicExponent, NULL, NULL);.. the corresponding Intel IPP version using ippsRSA_GenerateKeys goes like this:
IppsBigNumState* createBigNumState(int len, const Ipp32u* pData) {
int size;
ippsBigNumGetSize(len, &size);
IppsBigNumState* pBN = (IppsBigNumState*) ippMalloc(size);;
ippsBigNumInit(len, pBN);
if (pData != NULL) {
ippsSet_BN(IppsBigNumPOS, len, pData, pBN);
}
return pBN;
}
IppStatus RSA_IPPCrypto (int bitsRSA) {
IppStatus status;
// Security parameter specified for the
// Miller-Rabin test for probable primality.
int nTrials = 1;
// Number of bits of the exponent
int bitsExp = 24;
int sizeOfPrimeGen = -1;
int sizeOfRandomGen = -1;
int sizeOfPublicKey = -1;
int sizeOfPrivateKey = -1;
int sizeOfScratchBuffer = -1;
IppsPrimeState * primeGen = NULL;
IppsPRNGState * randomGen = NULL;
IppsRSAPublicKeyState * publicKey = NULL;
IppsRSAPrivateKeyState * privateKey = NULL;
Ipp8u * scratchBuffer = NULL;
Ipp32u E = 65537;
IppsBigNumState * pSrcPublicExp = createBigNumState (1, &E);
IppsBigNumState * pModulus = createBigNumState (bitsRSA / 32, NULL);
IppsBigNumState * pPublicExp = createBigNumState (bitsRSA / 32, NULL);
IppsBigNumState * pPrivateExp = createBigNumState (bitsRSA / 32, NULL);
// Prime Number Generator
ippsPrimeGetSize(bitsRSA, &sizeOfPrimeGen);
primeGen = (IppsPrimeState *) ippMalloc(sizeOfPrimeGen);
ippsPrimeInit(bitsRSA, primeGen);
// Pseudo Random Generator (default settings)
ippsPRNGGetSize(&sizeOfRandomGen);
randomGen = (IppsPRNGState*) ippMalloc (sizeOfRandomGen);
ippsPRNGInit(160, randomGen);
// Initialize the Public Key State
ippsRSA_GetSizePublicKey(bitsRSA, bitsExp, &sizeOfPublicKey);
publicKey = (IppsRSAPublicKeyState *)ippMalloc(sizeOfPublicKey);
ippsRSA_InitPublicKey(bitsRSA, bitsExp, publicKey, sizeOfPublicKey);
// Initialize the Private Key State
int bitsP = (bitsRSA + 1) / 2;
int bitsQ = bitsRSA - bitsP;
ippsRSA_GetSizePrivateKeyType2(bitsRSA, bitsRSA, &sizeOfPrivateKey);
privateKey = (IppsRSAPrivateKeyState *) ippMalloc(sizeOfPrivateKey);
ippsRSA_InitPrivateKeyType2(bitsP, bitsQ, privateKey, sizeOfPrivateKey);
// Initialize scratch buffer
ippsRSA_GetBufferSizePrivateKey(&sizeOfScratchBuffer, privateKey);
scratchBuffer = (Ipp8u *) ippMalloc (sizeOfScratchBuffer);
status = ippsRSA_GenerateKeys(
pSrcPublicExp,
pModulus, pPublicExp, pPrivateExp,
privateKey, scratchBuffer, nTrials,
primeGen, ippsPRNGen, randomGen
);
ippFree(pSrcPublicExp);
ippFree(pModulus);
ippFree(pPublicExp);
ippFree(pPrivateExp);
ippFree(primeGen);
ippFree(randomGen);
ippFree(publicKey);
ippFree(privateKey);
ippFree(scratchBuffer);
return status;
}Note that Intel IPP does not provide the implementation for conversion of the private and public keys into PEM format, and if one wants to implement those, must use an external software such as the ASN.1 Compiler to use the DER encoding to produce the PEM file. Therefore, the version of RSA key generation above, is incomplete at best.
Once we have a hands-on version of RSA generation, it is time for reckoning. I was interested to see how fast would
Intel IPP be over OpenSSL (assuming that IPP wins). To be fair, I decided to measure the performance in cycles in a
very fine-grained fashion, testing only ippsRSA_GenerateKeys and only RSA_generate_key, skipping any form of initialization.
A short description of the methodology goes as follows:
- Compile the code using
icpc composer_xe_2015.0.077on OS X Yosemite 10.10.5, running Intel(R) Core(TM) i7-3720Q CPU @ 2.60 GHz (Ivy Bridge). OpenSSL version is1.0.2d (9 Jul 2015). - Compile the code using
icpc composer_xe_2015.0.090on Debian 8.3, running Intel(R) Xeon(R) CPU E3-1285L v3 @ 3.10GHz. OpenSSL version is1.1.0-pre4 (beta)16 Mar 2016 - Compile the code using
-O3 -xHost -no-multibyte-chars, and consider single core implementation only. - Use
RDTSCas a timing infrastructure - Run each of the RSA generation functions 10 times, and average the runtimes.
- Repeat each 10 runs for 10 times, and take the median runtime as the final measure.
The obtained results (less is better) are given as follows (y-axis is logarithmic):
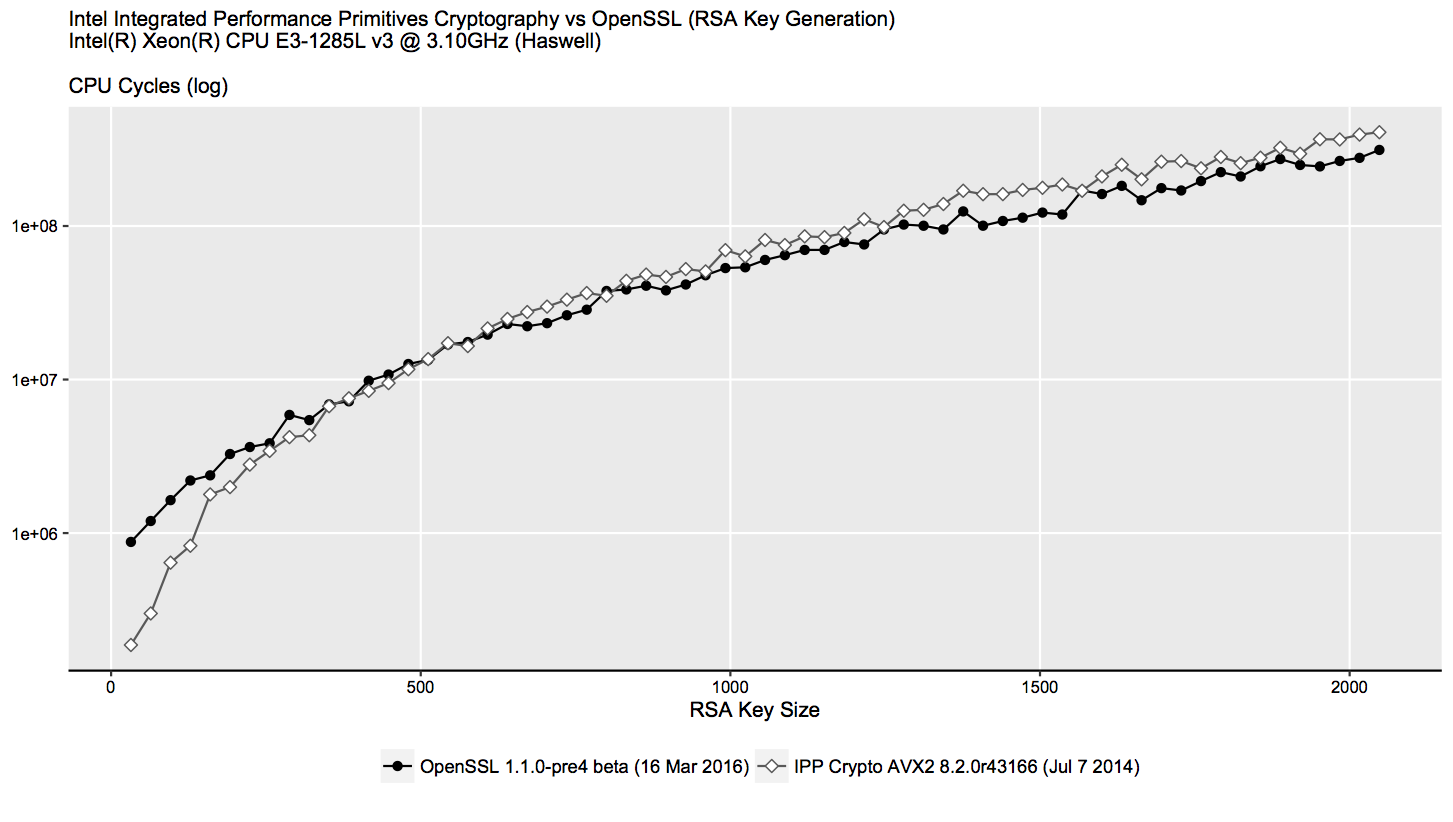
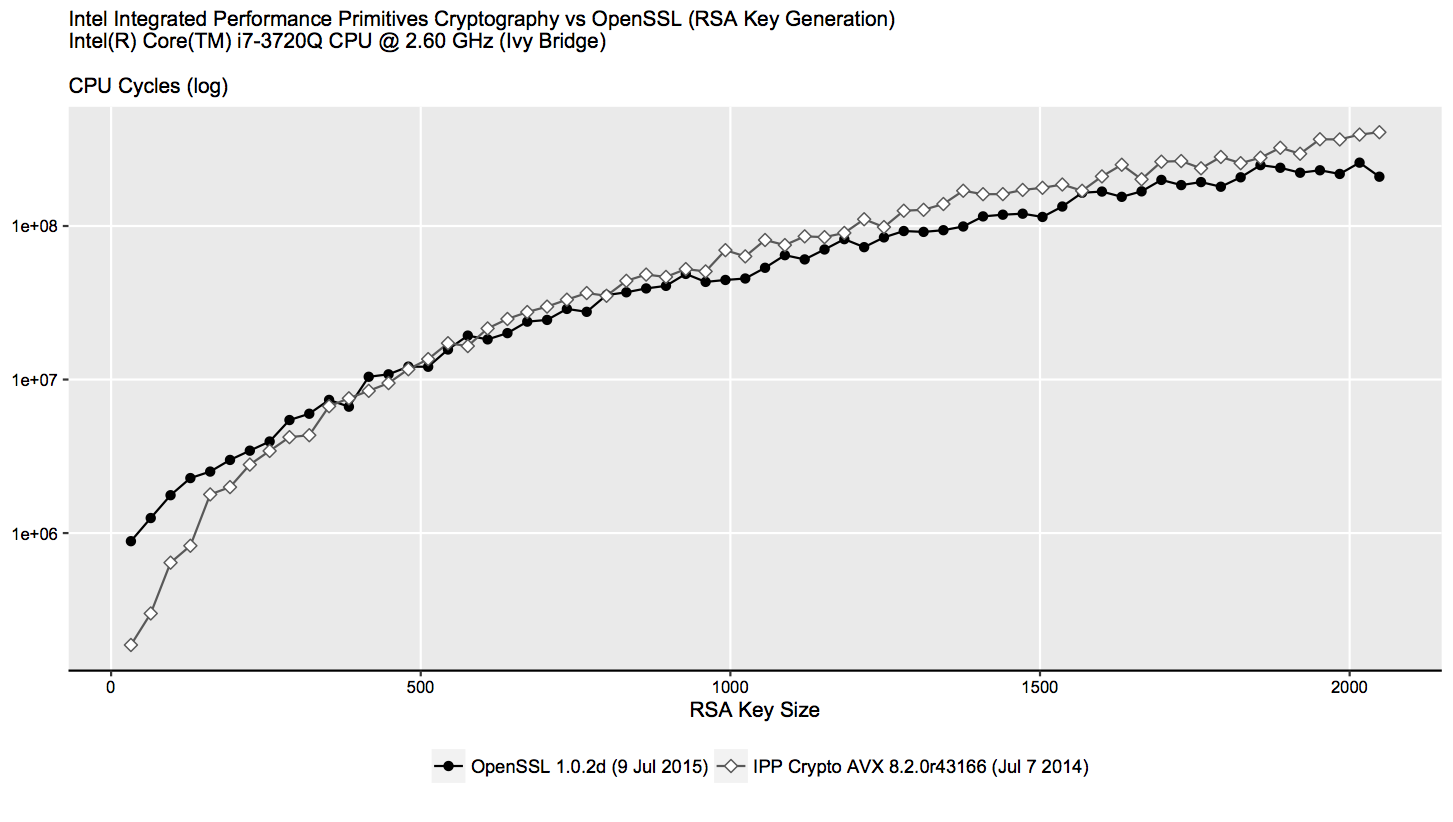
It seems that Intel IPP is only better generating keys which are less than 512 bits of length, while OpenSSL outperforms Intel IPP in almost all cases above 512 bits, generating the keys in less amount of CPU cycles. Considering that RSA keys of less than 1024 bytes are considered as insecure, these results, to my surprise, render the implementation of RSA key pair generation of Intel IPP obsolete.
To be fair, while I use the latest version of OpenSSL, this comparison does not reflect the latest version of Intel IPP. Also to note, I did not look into details to investigate the internal differences between the RSA key generation function in OpenSSL and Intel IPP. My observation is done strictly from the point of view of Intel IPP and OpenSSL user, where the only requirement is key pair generation.
For full transparency of this short experiment, the code for timing the two functions is available here, and the raw data (uses R to generate the plots) is available here.
