FGen: High-Performance Convolution Generator

FGen is a program generator for performance-optimized functions implementing convolutions, or FIR filters. The generator uses an internal mathematical DSL to enable structural optimization at a high level of abstraction. We use FGen as a testbed to demonstrate how to provide modular and extensible support for modern SIMD (single instruction, multiple data) vector architectures in a DSL-based generator.

Overview

Convolution of two vectors x and h

$x = (x_0, x_1, \ldots, x_{n-1})^T \text{ and } h = (h_0, h_1, \ldots, h_{k-1})^T$

is given with the following formula:

$y_m = \sum_{i=0}^{k-1} x_{m+(k-1)-i} \cdot h_i,\quad m = 0, \ldots, n-1.$

We use the language of media processing and call h the filter, k the number of taps, and the computation finite-impulse-response filter (FIR). The filter can also be viewed as a matrix vector product:

$y = x \ast h \Longleftrightarrow y = M_{n} (h) \cdot x,$

where M_{n}(h) is the n * n matrix:

$\begin{bmatrix} h_{k-1} & h_{k-2} & \cdots & h_{0} & & \\ & \ddots & \ddots & \ddots & \ddots & \\ & & h_{k-1} & h_{k-2} & \cdots & h_{0} \\ & & & h_{k-1} & \cdots & h_{1} \\ & & & & \ddots & \vdots \\ & & & & & h_{k-1} \\ \end{bmatrix}.$

In order to use the memory hierarchy, we could tile this matrix. The first observations is that the matrix can be broken down into two matrices. One that has parallelogram shape matrix (PFIR), and another one that is an upper triangular matrix (UTFIR). To express the breakdown formally, we use a mapping function, defined as:

$h^{n \rightarrow N}_{b}: i \mapsto b + i.$

and the notion of gathers and scatters defined in Figure 2 here. Then the breakdown is defined as:

$x\ast h = S(h^{n-k+1 \rightarrow n}_{0}) \cdot x \parallel h + S(h^{k-1 \rightarrow n}_{n-k+1}) \cdot \left[ G(h^{k-1 \rightarrow n}_{n - k + 1})\cdot x \bigtriangleup G(h^{k-1 \rightarrow k}_{1})\cdot h \right]$

Both PFIR and UTFIR can be tiled into smaller matrices. We can illustrate a the tiling of PFIR using:

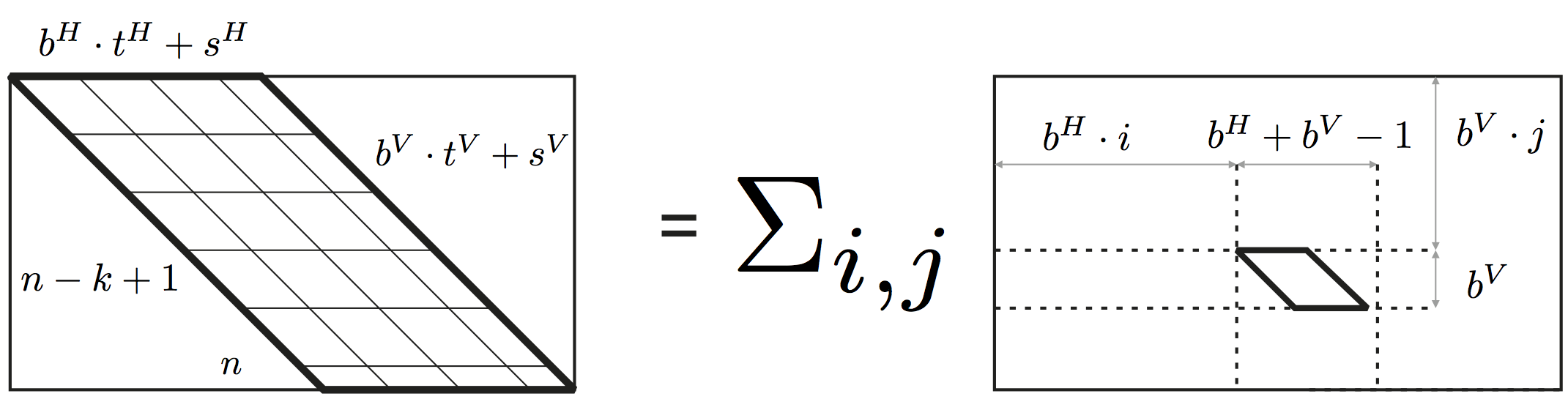
and similarly UTFIR:

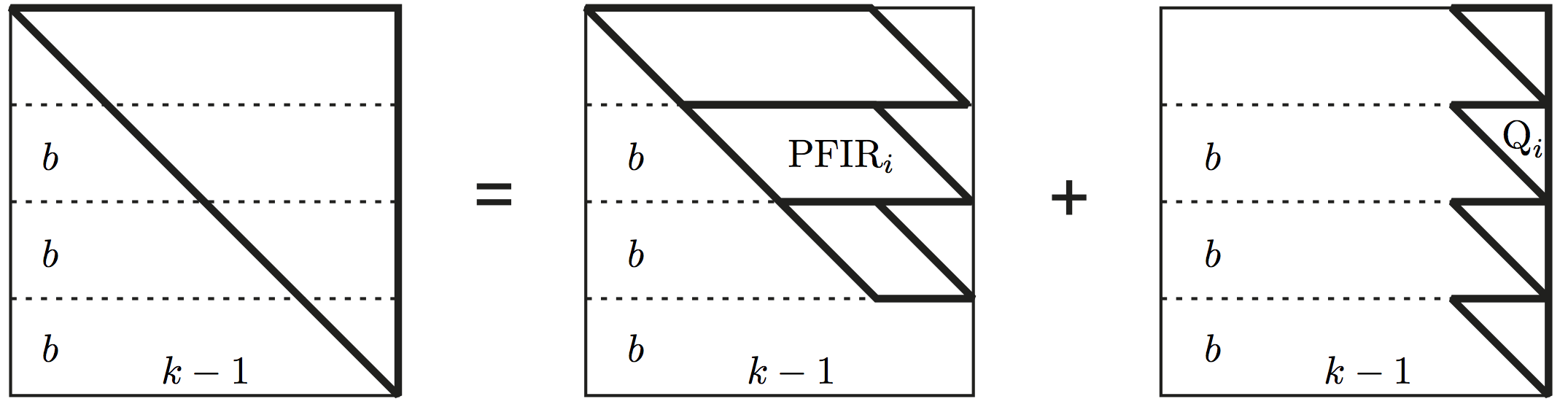
Formally, if $x \parallel h$ represent a PFIR filter (prallelogram shape matrix), then:

$\begin{array}{rcl} x \parallel h & = & \sum_{i=0}^{t^H-1} S(h^{b^H \rightarrow n-k+1}_{b^H \cdot i}) \sum_{j=0}^{t^V-1} (x_1 \parallel h_1) \\ & + & \sum_{i=0}^{t^H-1} S(h^{b^H \rightarrow n-k+1}_{b^H \cdot i}) (x_2 \parallel h_2 ) \\ & + & S(h^{s^H \rightarrow n-k+1}_{b^Ht^H}) \sum_{j=0}^{t^V-1} (x_3 \parallel h_1) \\ & + & S(h^{s^H \rightarrow n-k+1}_{b^Ht^H})( x_4 \parallel h_2 ) \end{array}$

where

$\begin{array}{lcllcl} x_1 & = & G(h^{b^H + b^V-1 \rightarrow n}_{b^H \cdot i + b^V \cdot j}) \cdot x & x_4 & = & G(h^{s^H + s^V - 1 \rightarrow n}_{b^Ht^H + b^Vt^V}) \cdot x \\ x_2 & = & G(h^{b^H + s^V-1 \rightarrow n}_{b^Vt^V + b^H \cdot i}) \cdot x & h_1 & = & G(h^{b^V \rightarrow k}_{k - b^V \cdot (j + 1)}) \cdot h \\ x_3 & = & G(h^{s^H + b^V - 1 \rightarrow n}_{b^Ht^H + b^V \cdot j}) \cdot x & h_2 & = & G(h^{s^V \rightarrow k}_{0}) \cdot h \\ \end{array}$

The breakdown of the UTFIR follows the similar formal expression that can be find here.

Loop optimizations

Loop optimizations such as loop merging, or loop unrolling are done at the $\Sigma$ -LL level using a rewrite system that fuses, for example data accesses. As one example,

$\sum_{i=0}^{p-1} S(h^{N_1 \rightarrow N}_{b}) \sum_{j=0}^{q-1} S(h^{n \rightarrow N_1}_{b\prime})$

is rewritten into

$\sum_{i=0}^{p-1} \sum_{j=0}^{q-1} S(h^{n \rightarrow N_1}_{b + b\prime}).$

Abstracting over Staging Decisions

Once all high level optimizations are exhausted on the higher-level IR (Intermediate Representation) of $\Sigma$ -LL, we lower the high level IR into a C-like IR that contains the low-level C code interleaved with vector instructions in the form of C-intrinsics.

Note that the high-level $\Sigma$ -LL IR deals with the pure mathematical abstractions of the convolution expression and its tiling. However, this abstract representation does not reason about the data type of the convolution expression, its memory layout, memory allocation or how the math maps to code or hardware instructions.

Therefore when lowering a high-level $\Sigma$ -LL expression, we might have to produce code that handles single or double precision floating point numbers, or integral numbers. The code could be vectorized by SSE or AVX, but could as well be a scalar code that handles left-over computations. According to the $\Sigma$ -LL transformations, a loop could be unrolled or not. And finally the intput can be consisted from real numbers or complex numbers, being interleaved or split in two memory locations. And finally, the code that we need to generate might be staged code or executed directly in the runtime.

The figure above depicts the different possibilities that could be taken to lower a high level $\Sigma$ -LL expression.

Represent Staging Decisions using Types LMS uses the type system to lift regular Scala code into staged code. To illustrate this process, we can consider a simple add function:

def add (a: Int, b: Int) = {
  a + b
}

To stage the function we only need to replace T with Rep[T]:

def add (a: Rep[Int], b: Rep[Int]) = {
  a + b
}

Looking at the two functions, we can observe that both functions have isomorphic bodies. This raises the question of whether it is possible to use the type system in decode the decision on whether we stage this function or not. Scala supports the definition of type aliases which can be used to define identity type function:

type Idt[T] = T // We will  use NoRep[T] = T instead of Idt[T] = T for simplicity

Therefore, the initial non-staged add function could as well be written as:

def add (a: Idt[Int], b: Idt[Int]) = {
  a + b
}

This result with the simple consequence that the higher kinded types Rep[_] and Idt[_] can be used as decision of whether a given code is staged or not. To abstract that decision we can use:

def add [R[_]] (a: R[Int], b: R[Int]) = {
  a + b
}

This allows us to plug Rep[_] and obtain staged function, or use Idt[_] and deal with regular function.

Representing Scalar or Vector Primitive Types Scalar primitive types are already represented in the type system of Scala (well at least the signed types, as the JVM is missing unsigned types). However, neither Scala nor the JVM has no notion for SIMD type primitives.

__m64   // MMX integer types
__m128  // SSE 4x32-bit float
__m128d // SSE 2x64-bit float
__m128i // SSE 2x64/4x32/8x16/16x8-bit integer
__m256  // AVX 8x32-bit float
__m256d // AVX 4x64-bit float
__m256i // AVX 4x64/84x32/16x16/32x8-bit integer
__m512  // AVX512 16x32-bit float
__m512d // AVX512 8x64-bit float
__m512i // AVX512 8x64/16x32/32x16/64x8-bit integer

Looking at the SIMD primitives however, we can notice that each of those represent continious memory block of a given primitive. Therefore, we can simply represent them with a generic type called Packed[T] such that T corresponds to a given scalar primitive. Finally, using the identity type explaned before, we can use the same trick to represent both the SIMD and calar primitives:

type Single[T] = T
abstract Packed[T]

This allows us to abstract Single[_] and Packed[_] using higher kinded types, as explained before.

Abstracting Primitives. So far we have defined the basis of representing the scalar and the vector types. But to use them, we also need to define the operations performed on the same types. We can do this using type classes inspired by Numeric[T] in Scala. Instead of Numeric[T] we define:

abstract class NumericOps[T:Manifest] {
  def plus       (x: T, y: T) : T
  def minus      (x: T, y: T) : T
  def times      (x: T, y: T) : T
  def interleave (x: T, y: T) : (T, T)
  def unravel    (x: T, y: T) : (T, T)

  class Ops(lhs: T) {
    def +(rhs: T) = plus (lhs, rhs)
    def -(rhs: T) = minus(lhs, rhs)
    def *(rhs: T) = times(lhs, rhs)
  }
  implicit def mkNumericOps(lhs: T): Ops = new Ops(lhs)
}

This allows us to easily define extension to the NumericOps class that deals with non-staged code involving scalar primitives:

class NumericNoRepOps[T:Numeric:Manifest] extends NumericOps[NoRep[Single[T]]]  {
  def plus       (x : T, y : T) = implicitly[Numeric[T]].plus (x, y)
  def minus      (x : T, y : T) = implicitly[Numeric[T]].minus(x, y)
  def times      (x : T, y : T) = implicitly[Numeric[T]].times(x, y)
  def interleave (x : T, y : T) = (x, y)
  def unravel    (x : T, y : T) = (x, y)
  def fromDouble (x: Double): T = convert[Double, T](x)
}

… or staged scalars primitives:

class NumericRepOps[T:Numeric:Manifest] extends NumericOps[Rep[Single[T]]] {
  def plus       (x : Rep[T], y : Rep[T]) = numeric_plus [T](x, y)
  def minus      (x : Rep[T], y : Rep[T]) = numeric_minus[T](x, y)
  def times      (x : Rep[T], y : Rep[T]) = numeric_times[T](x, y)
  def interleave (x : Rep[T], y : Rep[T]) = (x, y)
  def unravel    (x : Rep[T], y : Rep[T]) = (x, y)
  def fromDouble (x: Double): Rep[T] = Const[T](convert[Double, T](x))
}

… or even vector operations:

class PackedNumericOps[T:Numeric:Manifest] extends NumericOps[Rep[Packed[T]]]  {
  private val vsize = codegen.getInstructionSetVectorSize[T]
  val m = implicitly[Manifest[T]]
  def plus       (x : Rep[Packed[T]], y : Rep[Packed[T]]) = infix_vadd[T](x, y)
  def minus      (x : Rep[Packed[T]], y : Rep[Packed[T]]) = infix_vsub[T](x, y)
  def times      (x : Rep[Packed[T]], y : Rep[Packed[T]]) = infix_vmul[T](x, y)
  def interleave (x : Rep[Packed[T]], y : Rep[Packed[T]]) = m.toString() match {
    case "Int" | "Float" => codegen.instructionSet match {
      case SSE | SSE2 | SSE3 | SSE3 | SSE41 | SSE42 | AVX => {
        val inm1 = (2 << 6) + (0 << 4) + (2 << 2) + (0 << 0)
        val inm2 = (3 << 6) + (1 << 4) + (3 << 2) + (1 << 0)
        (infix_shuffle[T](x, y, inm1), infix_shuffle[T](x, y, inm2))
      }
    }
    case "Double" => codegen.instructionSet match {
      case SSE2 | SSE3 | SSE3 | SSE41 | SSE42 | AVX =>
        (infix_unpack_low[T](x, y), infix_unpack_high[T](x, y))
    }
  }
  def unravel(x : Rep[Packed[T]], y : Rep[Packed[T]]) = m.toString() match {
    case "Int" | "Float" => codegen.instructionSet match {
      case SSE | SSE2 | SSE3 | SSE3 | SSE41 | SSE42 | AVX =>
        (infix_unpack_low[T](x, y), infix_unpack_high[T](x, y))
    }
    case "Double" => codegen.instructionSet match {
      case SSE2 | SSE3 | SSE3 | SSE41 | SSE42 | AVX =>
        (infix_unpack_low[T](x, y), infix_unpack_high[T](x, y))
    }
  }
}

The 3 classes above are the basis for the rest of our further implementation.

Abstracting Complex/Real elements Since our requirements demands us to reason about complex or real numbers, we abstract the two options using;

abstract class Element [+T] {}
case class Real    [+T] (_re: T)         extends Element[T] {}
case class Complex [+T] (_re: T, _im: T) extends Element[T] {}

And similarly to the abstraction defined for NumericOps we abstract on top of the Element class:

abstract class ElementOps[ElementClass[_], T: NumericOps]
    (implicit m: Manifest[ElementClass[T]]) { self =>

  def plus    (x: ElementClass[T], y: ElementClass[T]): ElementClass[T]
  def minus   (x: ElementClass[T], y: ElementClass[T]): ElementClass[T]
  def times   (x: ElementClass[T], y: ElementClass[T]): ElementClass[T]

  class Ops(lhs: ElementClass[T]) {
    def +(rhs: ElementClass[T]) = plus (lhs, rhs)
    def -(rhs: ElementClass[T]) = minus(lhs, rhs)
    def *(rhs: ElementClass[T]) = times(lhs, rhs)
  }
  implicit def mkElementOps(lhs: ElementClass[T]): Ops = new Ops(lhs)
}

You will notice that the ElementOps abstraction expects the ElementClass to have T as an underlying type, and has the NumericOps as an implicit case class parameter. Similarly to Numeric in Scala, we can use this class to generalize the computations:

class ComplexOps[T:Manifest](implicit nops: NumericOps[T]) extends ElementOps[Complex, T] { import nops._
  def plus  (x: Complex[T], y: Complex[T]) = Complex(x._re + y._re, x._im + y._im)
  def minus (x: Complex[T], y: Complex[T]) = Complex(x._re - y._re, x._im - y._im)
  def times (x: Complex[T], y: Complex[T]) = {
    val m1 = x._re * y._re
    val m2 = x._im * y._im
    val m3 = x._re * y._im
    val m4 = x._im * y._re
    Complex(m1 - m2, m3 + m4)
  }
  def extract (elem: Complex[T]) = List(elem._re, elem._im)
}

We can observe that the complex abstraction does not have to reason whether the underlying primitives are of a particular type, or whether are vectorized or not. It will simply use the NumericOps class to do the job. The abstraction that represents the real numbers is implemented similarly.

Abstracting Memory Layout To achieve this, we need to abstract through the operations performed on a given array. Therefore:

/**
 * @tparam V Staged array or not
 * @tparam R Element staged or not
 * @tparam P Packed or single
 * @tparam A Staged/non-staged and/or packed/single elements
 * @tparam T Primitives type
 */
abstract class ArrayOps[V[_], R[_], P[_], A[_], T] {
  def alloc  (s: V[Int]): V[Array[A[T]]]
  def apply  (x: V[Array[A[T]]], i: V[Int]): R[P[T]]
  def update (x: V[Array[A[T]]], i: V[Int], y: R[P[T]])
}

This allows us to define several arrays of different structure, the first being just staged array:

class StagedSingleArrayOps[T:Manifest] extends ArrayOps[Rep, Rep, Single, NoRep, T] {
  def alloc (s: Rep[Int]): Rep[Array[T]] = array_obj_new[T](s)
  def apply (x: Rep[Array[T]], i: Rep[Int]): Rep[T] = array_apply[T](x,i)
  def update(x: Rep[Array[T]], i: Rep[Int], y: Rep[T]) = array_update[T](x,i,y)
}

… we can as well define an array of staged scalar elements:

class ScalarSingleArrayOps[T:Manifest] extends ArrayOps[NoRep, Rep, Single, Rep, T] {
  def alloc (s: NoRep[Int]): Array[Rep[T]] = new Array[Rep[T]](s)
  def apply (x: Array[Rep[T]], i: NoRep[Int]): Rep[T] = x(i)
  def update(x: Array[Rep[T]], i: NoRep[Int], y: Rep[T]) = x.update(i,y)
}

… or a staged vector array (i.e. each load results with a vector type, and each store is done with a vector type):

class StagedPackedArrayOps[T:Manifest] extends ArrayOps[Rep, Rep, Packed, NoRep, T] {
  val vecLength = codegen.getInstructionSetVectorSize[T]
  def alloc (s: Rep[Int]): Rep[Array[T]] = array_obj_new(s)
  def apply (x: Rep[Array[T]], i: Rep[Int]): Rep[Packed[T]] = infix_vload[T](x, i, vecLength)
  def update(x: Rep[Array[T]], i: Rep[Int], y: Rep[Packed[T]]) = infix_vstore(x, i, y)
}

Putting it all Together Finally, once we have all pieces of the abstraction we are able to build one single vector abstraction that is able to abstract all requirements:

abstract class CVector[V[_], E[_], R[_], P[_], T] (implicit
  val aops: ArrayOps[V, R, P, E, T]
  val eops: ElementOps[E, R[P[T]]],
  val nops: NumericOps[R[P[T]]],
) { self =>
  def apply  (i: V[Int]): E[R[P[T]]]
  def update (i: V[Int], y: E[R[P[T]]])
  def size   (): V[Int]
}

We call the abstraction CVector, as we generate C code, and our goal is to represent a C vector structure with different instatiations. Finally, if we want to use this function to simply perform additions, we write the following code:

def add[V[_], E[_], R[_], P[_], T] (
    x: CVector[V, E, R, P, T],
    y: CVector[V, E, R, P, T],
    z: CVector[V, E, R, P, T]
) = for ( i <- 0 until x.size() ) {
  z(i) = x(i) + y(i)
}

Depending on the type instatiation, the same code can end up having many different forms, as illustrated in Figure 4 taken from Abstracting Vector Architectures in Library Generators: Case Study Convolution Filters:

While performing a sum is quite straight forward, the real power of this abstraction is once performing the lowering step of $\Sigma$ -LL into C-IR.

class SigmaLL2IIRTranslator[E[_], R[_], P[_], T] {
  type Element = E[R[P[T]]]
  def sum (in: List[Element]) =
    if (in.length == 1) in(0) else {
      val (m, e) = (in.length / 2, in.length)
      sum(in.slice(0, m)) + sum(in.slice(m, e))
    }
  def translate(stm: Stm) = stm match {
    case TP(y, PFIR(x, h)) =>
      val xV = List.tabulate(k)(i => x.apply(i))
      val hV = List.tabulate(k)
               (i => h.vset1(h.apply(k-i-1)))
      val tV = (xV, hV).zipped map (_*_)
      y.update(y(0), sum(tV))
  }
}

In fact, the single codebase defined above, is capable or generating code that is AVX, SSE or scalar code, that operates with real or complex numbers, having loop or unrolled code, performing the computation using floats, doubles or integers.

Results

We benchmarked on two machines, Intel(R) Xeon(R) CPU E5-2643 3.3 GHz supporting AVX, running Ubuntu 13.10, kernel v3.11.0-12-generic, and Intel(R) Core(TM)2 Duo CPU L7500 1.6GHz supporting SSSE3, running Debian 7, kernel v3.2.0-4-686-pae. Intel’s Hyper-Threading, Turbo Boost (Xeon) and Intel Dynamic Acceleration (Core2) were disabled on both machines during the tests. We compare against convolutions from Intel IPP v8.0.1 and Intel MKL v11.1.1.

As base line we also include a straightforward implementation of convolution: a double loop with fixed array sizes. All code is compiled using the Intel C++ Composer 2013.SP1.1.106, with flags -std=c99 -O3 -xHost.

We only consider double precision code (4-way on AVX and 2-way on SSSE3). The input sizes, related to the input vector of the convolution expression, are powers of two in the form of $n = 512 \cdot 2^i$ for $i = 1, \ldots, 16$ to ensure a sampling of all cache levels for both machines. For each machine we perform two types of tests:

All vectors are arrays of real numbers, and the filter size is 8 or 20;
All vectors are arrays of interleaved complex numbers, and the filter size is 8 or 20 (complex numbers).

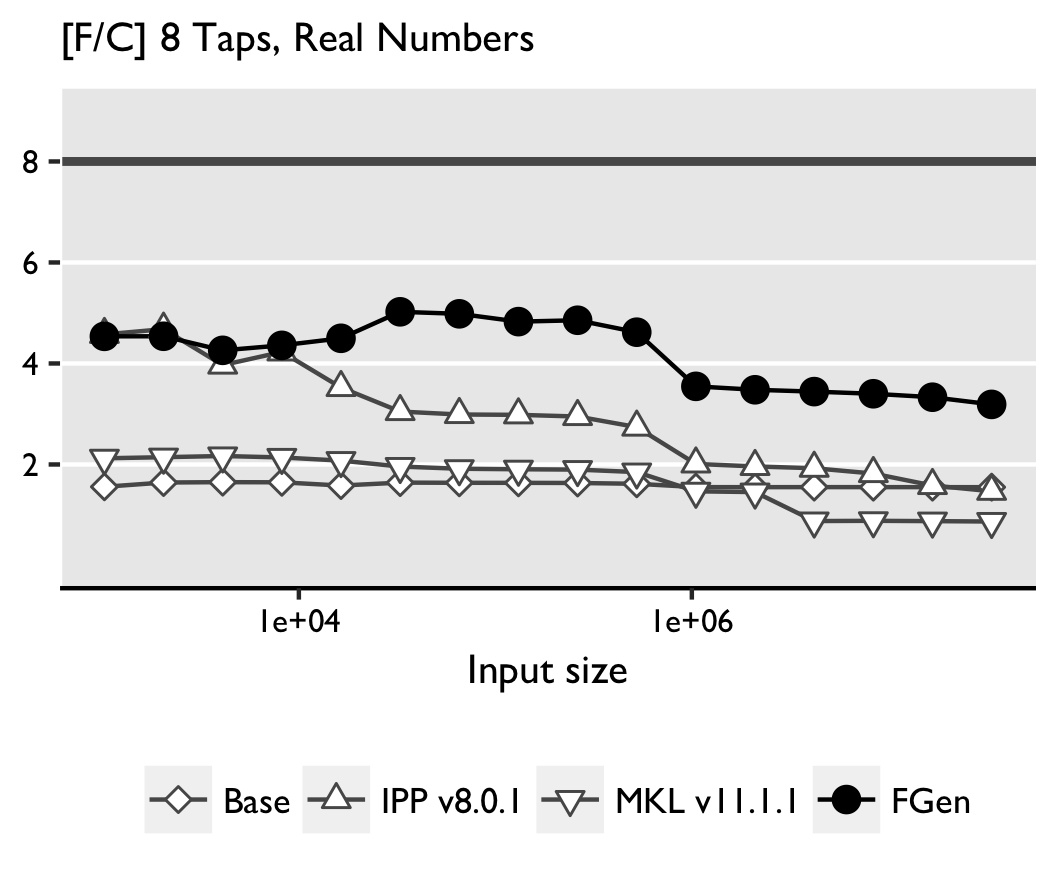
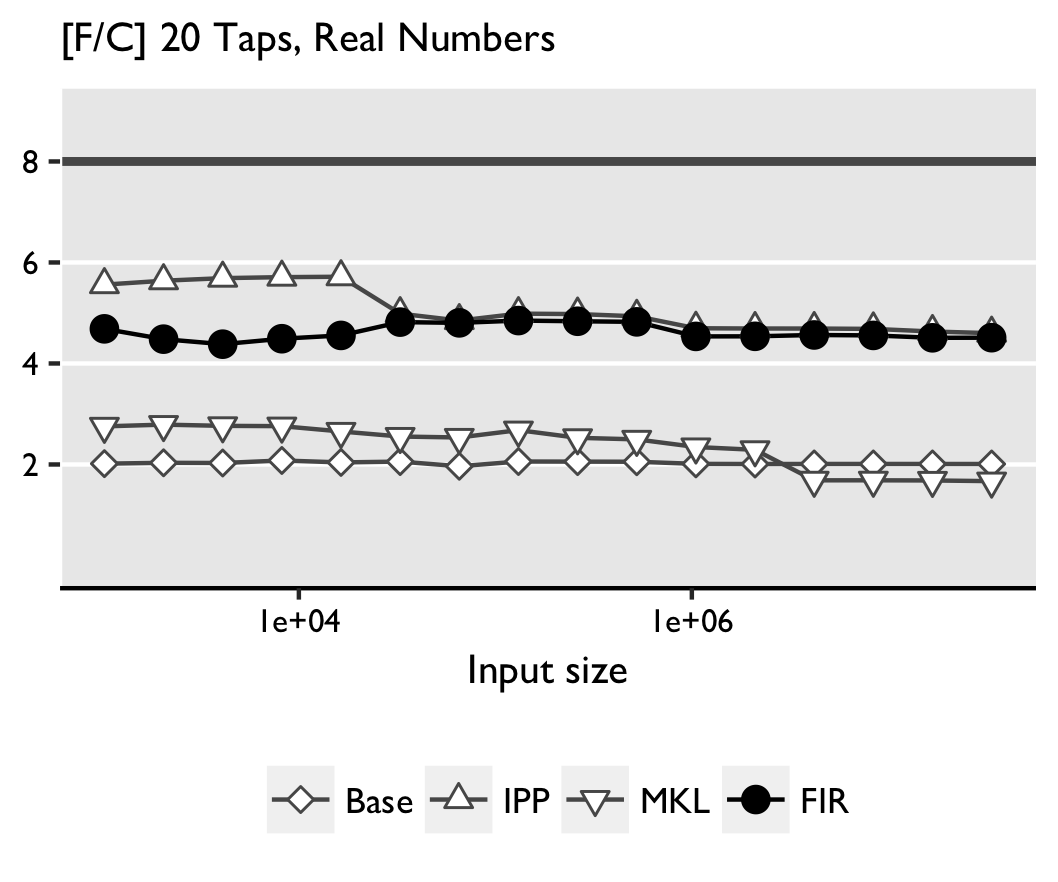
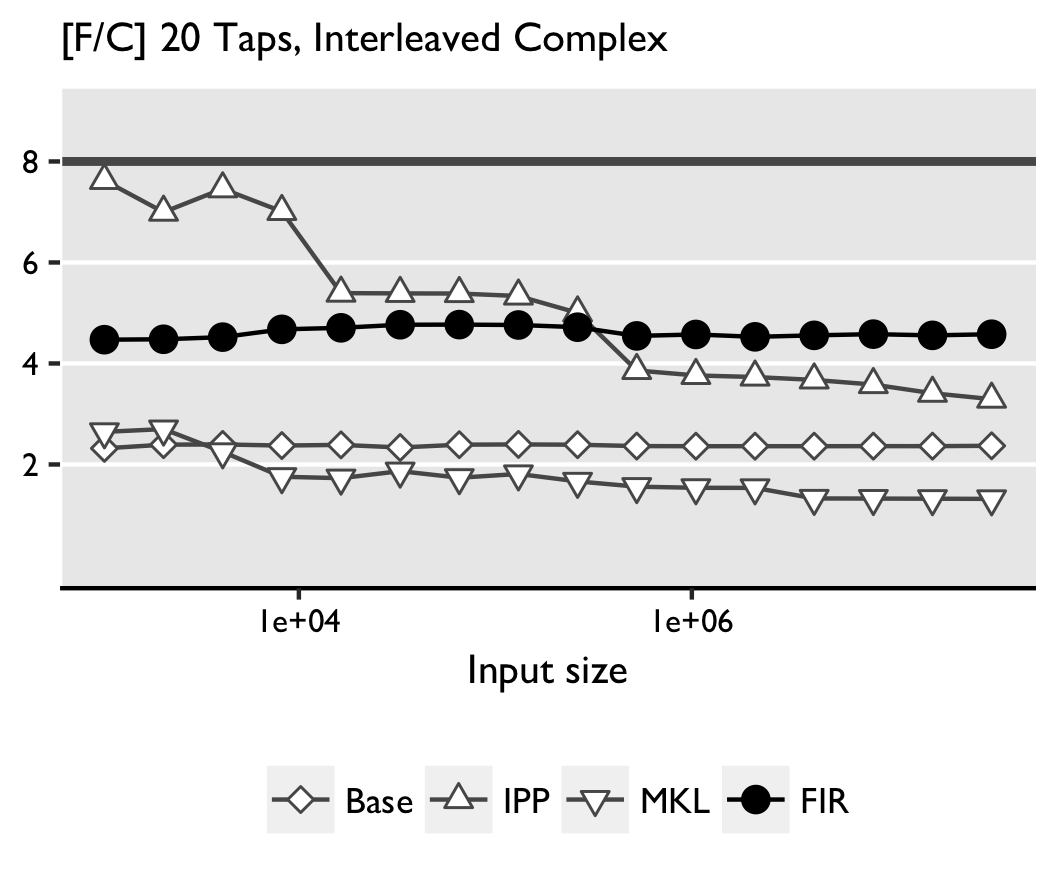
Time is measured under warm-cache conditions, using a two loops measuring strategy. The inner loop measures time as the mean of sufficently many iteration; the outer loop returns the median of several such runs. The results of Intel(R) Xeon(R) CPU E5-2643 3.3 GHz are shown below:

Tests obtained with Intel(R) Core(TM)2 Duo CPU L7500 1.6GHz are sown below:

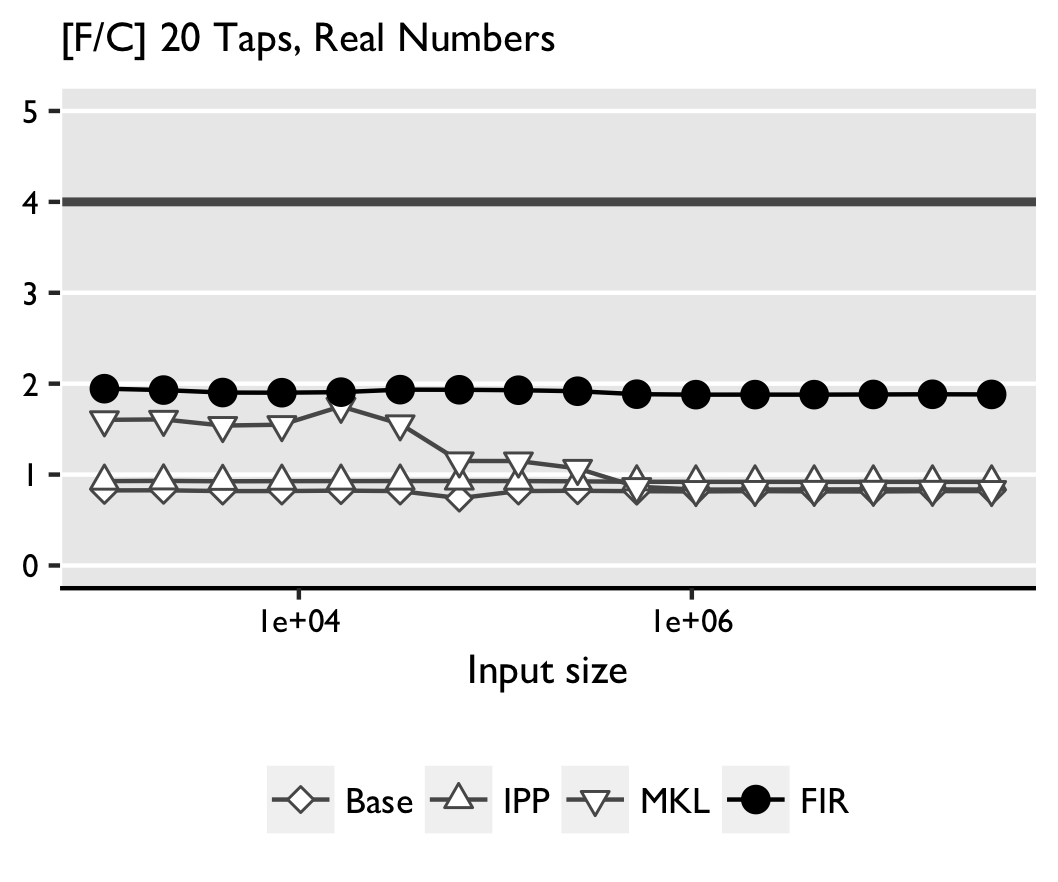
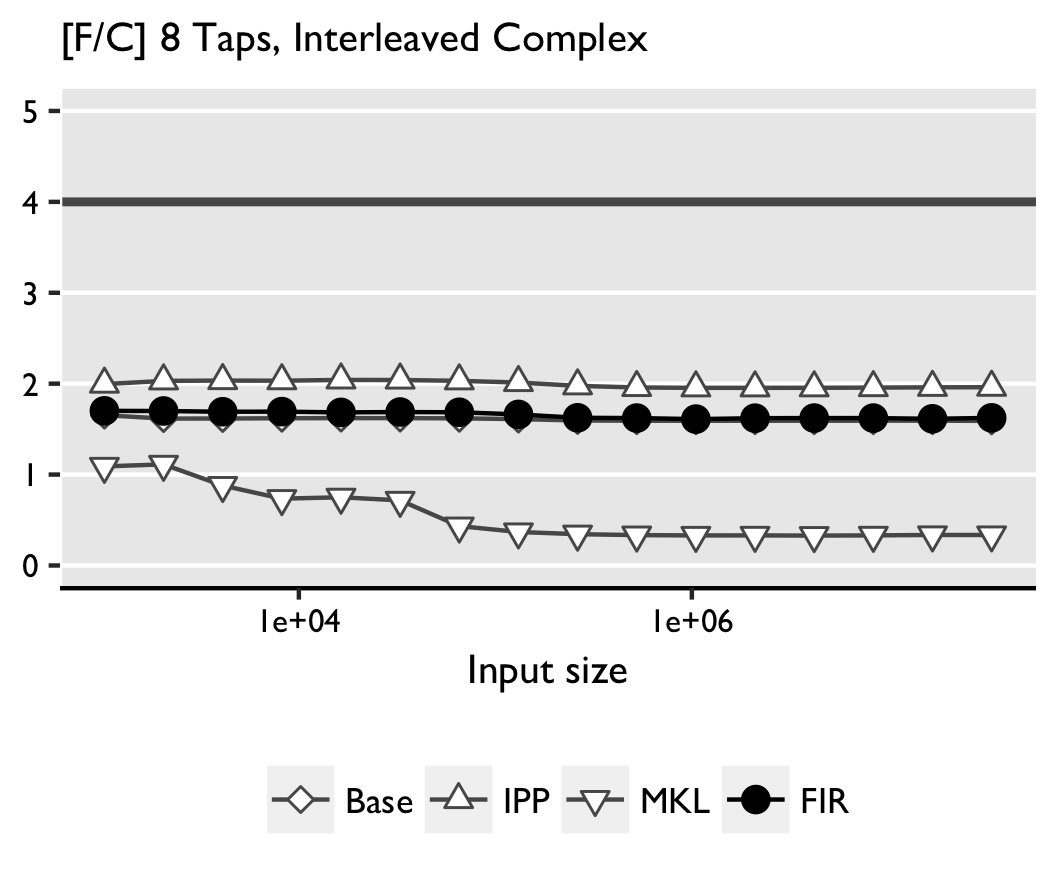
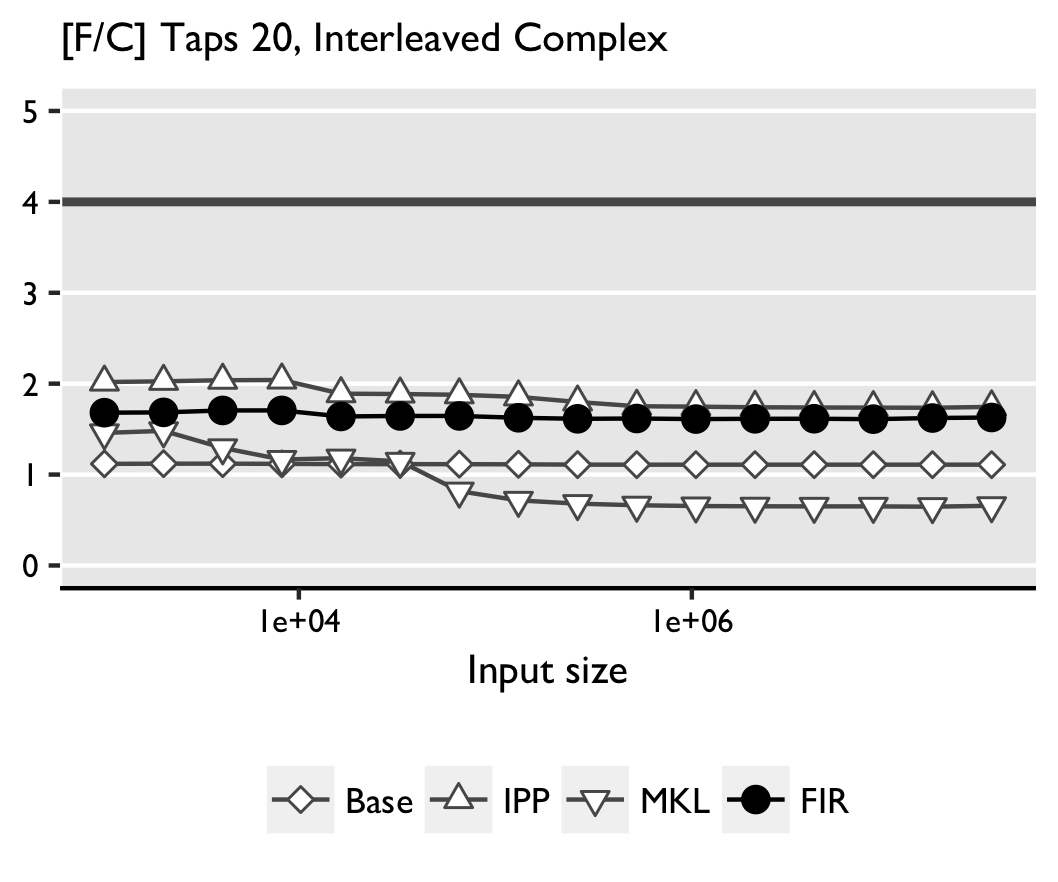
Real convolution. FGen-generated code outperforms the other implementations, except IPP for small sizes and 20 taps. The reason is not clear as the code is distributed as binary, which prevents inspection. In some cases MKL performs worse than the base implementation. Apparently, icc can efficiently optimize and vectorize the simple double loop with fixed bounds.

Complex convolution. For large sizes FGen-generated code is faster (AVX) or roughly competitive (SSSE3) with the next best IPP. Again, MKL performs worse than the straightline code with a similar possible explanation as above. We note that in FGen there is further room for improvement in the shuffling needed to work on interleaved data. We believe that the gains for larger sizes on AVX are due to a more thorough exploration of the possible tiling strategies in FGen.

If you want to learn more about this work, check out our paper titled Abstracting Vector Architectures in Library Generators: Case Study Convolution Filters, or check out the slides of the talk given at ARRAY’14 available at the blog post here.